Central Tendency | Understanding the Mean, Median & Mode
Measures of central tendency help you find the middle, or the average, of a dataset. The 3 most common measures of central tendency are the mode, median, and mean.
- Mode: the most frequent value.
- Median: the middle number in an ordered dataset.
- Mean: the sum of all values divided by the total number of values.
In addition to central tendency, the variability and distribution of your dataset is important to understand when performing descriptive statistics.
Distributions and central tendency
A dataset is a distribution of n number of scores or values.
Normal distribution
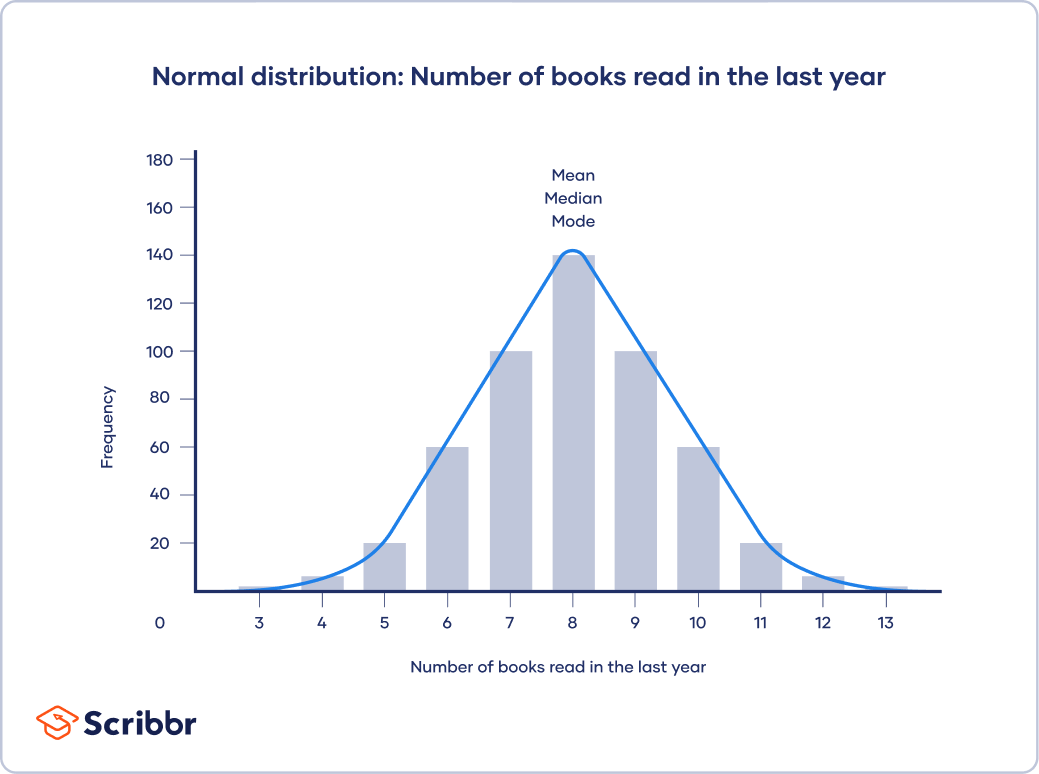
In a normal distribution, data is symmetrically distributed with no skew. Most values cluster around a central region, with values tapering off as they go further away from the center. The mean, mode and median are exactly the same in a normal distribution.
A histogram of your data shows the frequency of responses for each possible number of books. From looking at the chart, you see that there is a normal distribution.
The mean, median and mode are all equal; the central tendency of this dataset is 8.
Skewed distributions
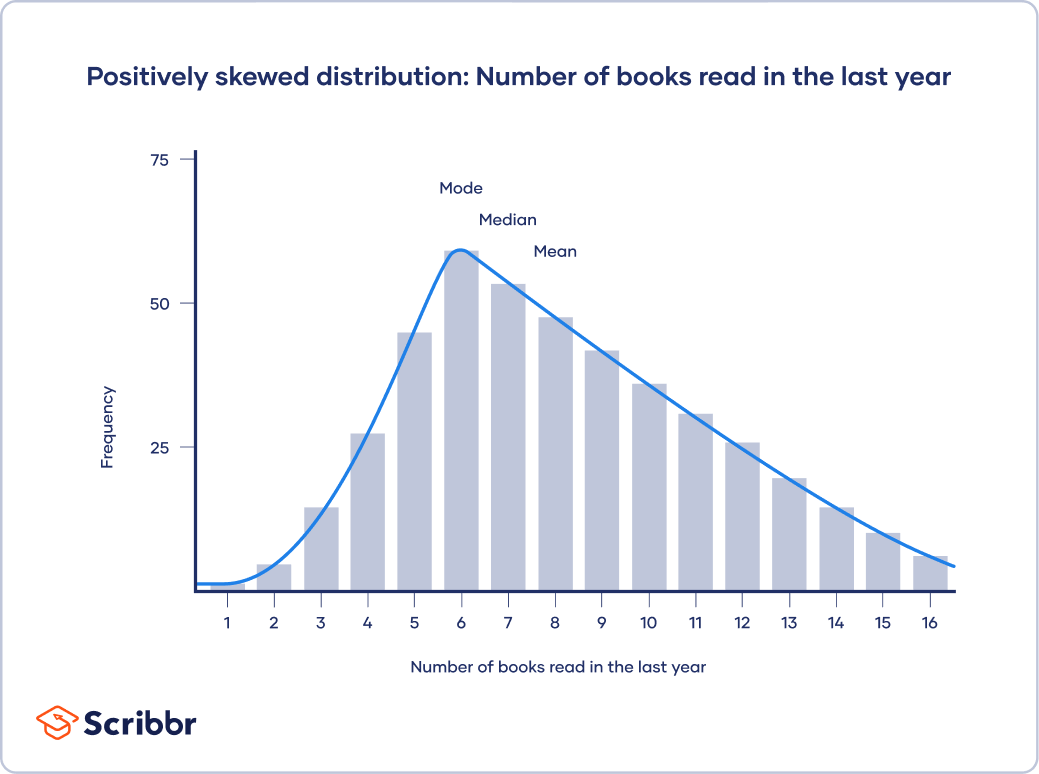
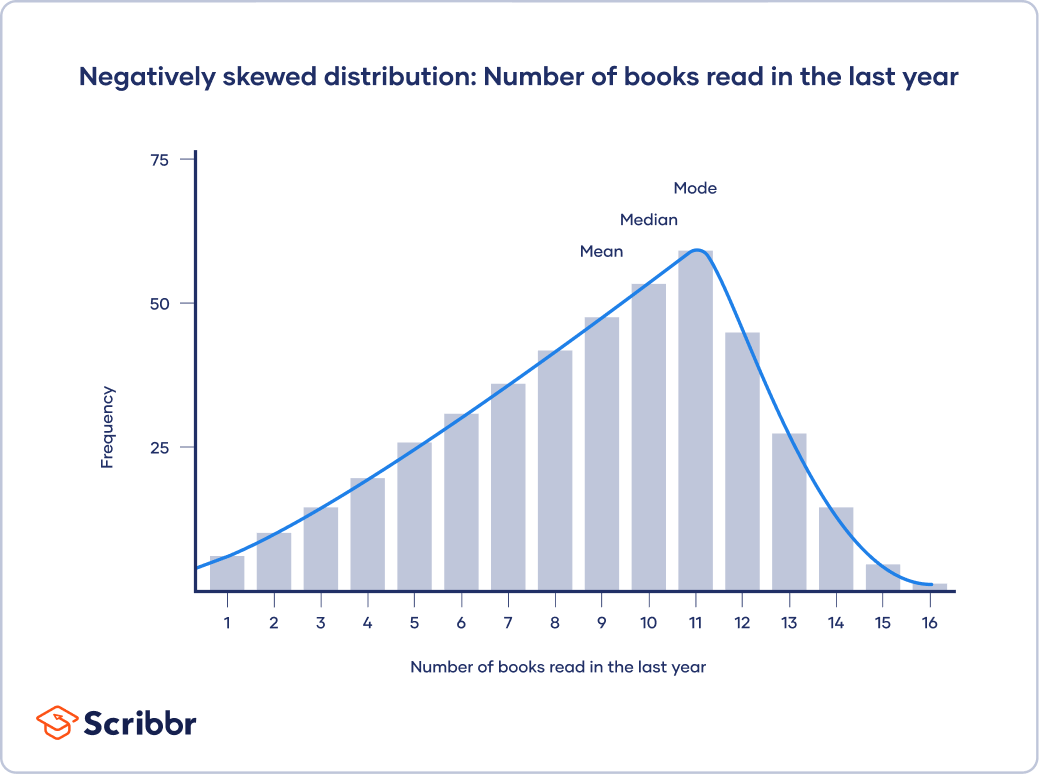
In skewed distributions, more values fall on one side of the center than the other, and the mean, median and mode all differ from each other. One side has a more spread out and longer tail with fewer scores at one end than the other. The direction of this tail tells you the side of the skew
In a positively skewed distribution, there’s a cluster of lower scores and a spread out tail on the right. In a negatively skewed distribution, there’s a cluster of higher scores and a spread out tail on the left.
In this histogram, your distribution is skewed to the right, and the central tendency of your dataset is on the lower end of possible scores.
In a positively skewed distribution, mode < median < mean.
In a negatively skewed distribution, mean < median < mode.
Mode
The mode is the most frequently occurring value in the dataset. It’s possible to have no mode, one mode, or more than one mode.
To find the mode, sort your dataset numerically or categorically and select the response that occurs most frequently.
To find the mode, sort your data by category and find which response was chosen most frequently.
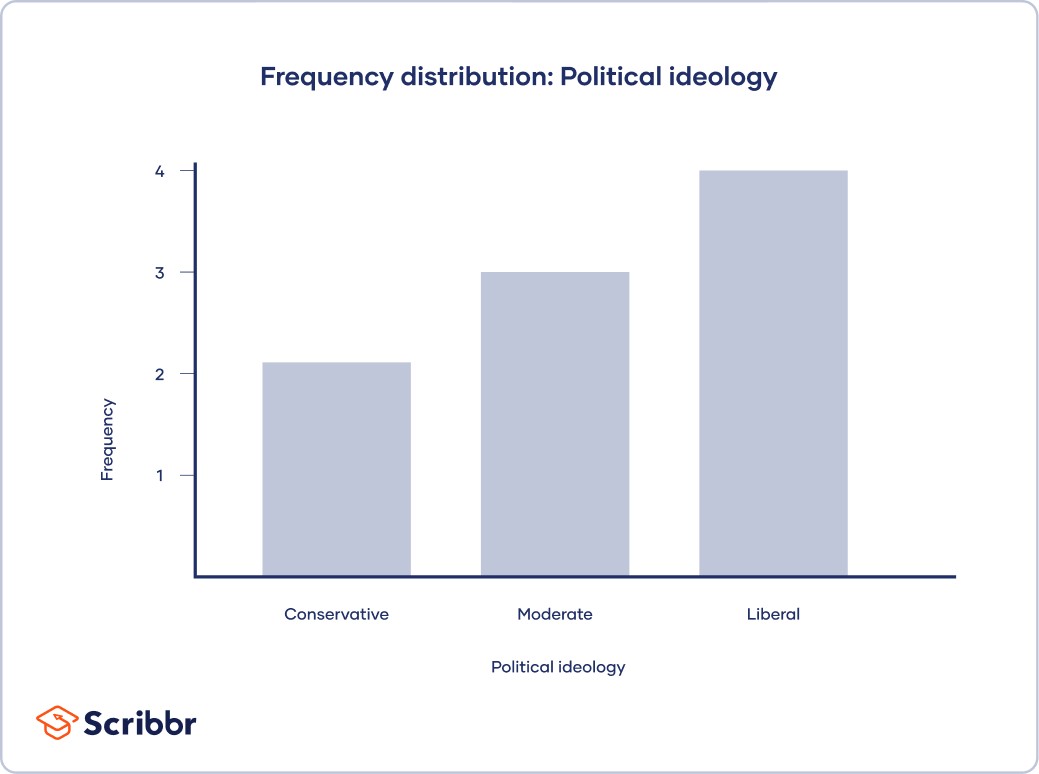
To make it easier, you can create a frequency table to count up the values for each category.
| Political ideology | Frequency |
|---|---|
| Conservative | 2 |
| Moderate | 3 |
| Liberal | 4 |
Mode: Liberal
The mode is easily seen in a bar graph because it is the value with the highest bar.
When to use the mode
The mode is most applicable to data from a nominal level of measurement. Nominal data is classified into mutually exclusive categories, so the mode tells you the most popular category.
For continuous variables or ratio levels of measurement, the mode may not be a helpful measure of central tendency. That’s because there are many more possible values than there are in a nominal or ordinal level of measurement. It’s unlikely for a value to repeat in a ratio level of measurement.
| Participant | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Reaction time (milliseconds) | 267 | 345 | 421 | 324 | 401 | 312 | 382 | 298 | 303 |
In this dataset, there is no mode, because each value occurs only once.
Median
The median of a dataset is the value that’s exactly in the middle when it is ordered from low to high.
| Participant | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Speed | Medium | Slow | Fast | Fast | Medium | Fast | Slow |
To find the median, you first order all values from low to high. Then, you find the value in the middle of the ordered dataset – in this case, the value in the 4th position.
| Ordered dataset | Slow | Slow | Medium | Medium | Fast | Fast | Fast |
|---|
Median: Medium
In larger datasets, it’s easier to use simple formulas to figure out the position of the middle value in the distribution. You use different methods to find the median of a dataset depending on whether the total number of values is even or odd.
Median of an odd-numbered dataset
For an odd-numbered dataset, find the value that lies at the position, where n is the number of values in the dataset.
| Reaction time (milliseconds) | 287 | 298 | 345 | 365 | 380 |
|---|
The middle position is calculated using , where n = 5.
That means the median is the 3rd value in your ordered dataset.
Median: 345 milliseconds
Median of an even-numbered dataset
For an even-numbered dataset, find the two values in the middle of the dataset: the values at the and
positions. Then, find their mean.
| Reaction time (milliseconds) | 287 | 298 | 345 | 357 | 365 | 380 |
|---|
The middle positions are calculated using and
, where n = 6.
That means the middle values are the 3rd value, which is 345, and the 4th value, which is 357.
To get the median, take the mean of the 2 middle values by adding them together and dividing by 2.
Median: 351 milliseconds
Mean
The arithmetic mean of a dataset (which is different from the geometric mean) is the sum of all values divided by the total number of values. It’s the most commonly used measure of central tendency because all values are used in the calculation.
| Participant | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Reaction time (milliseconds) | 287 | 345 | 365 | 298 | 380 |
First you add up the sum of all values:
Then you calculate the mean using the formula
There are 5 values in the dataset, so n = 5.
Mean (x̄): 335 milliseconds
Outlier effect on the mean
Outliers can significantly increase or decrease the mean when they are included in the calculation. Since all values are used to calculate the mean, it can be affected by extreme outliers. An outlier is a value that differs significantly from the others in a dataset.
| Participant | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Reaction time (milliseconds) | 832 | 345 | 365 | 298 | 380 |
Due to the outlier, the mean () becomes much higher, even though all the other numbers in the dataset stay the same.
Mean: 444 milliseconds
Population versus sample mean
A dataset contains values from a sample or a population. A population is the entire group that you are interested in researching, while a sample is only a subset of that population.
While data from a sample can help you make estimates about a population, only full population data can give you the complete picture.
In statistics, the notation of a sample mean and a population mean and their formulas are different. But the procedures for calculating the population and sample means are the same.
- x̄: sample mean
: sum of all values in the sample dataset
- n: number of values in the sample dataset
- μ: population mean
: sum of all values in the population dataset
- N: number of values in the population dataset
When should you use the mean, median or mode?
The 3 main measures of central tendency are best used in combination with each other because they have complementary strengths and limitations. But sometimes only 1 or 2 of them are applicable to your dataset, depending on the level of measurement of the variable.
- The mode can be used for any level of measurement, but it’s most meaningful for nominal and ordinal levels.
- The median can only be used on data that can be ordered – that is, from ordinal, interval and ratio levels of measurement.
- The mean can only be used on interval and ratio levels of measurement because it requires equal spacing between adjacent values or scores in the scale.
| Levels of measurement | Examples | Measure of central tendency |
|---|---|---|
| Nominal |
|
|
| Ordinal |
|
|
| Interval and ratio |
|
|
To decide which measures of central tendency to use, you should also consider the distribution of your dataset.
For normally distributed data, all three measures of central tendency will give you the same answer so they can all be used.
In skewed distributions, the median is the best measure because it is unaffected by extreme outliers or non-symmetric distributions of scores. The mean and mode can vary in skewed distributions.
Frequently asked questions
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.
Bhandari, P. (2022, December 31). Central Tendency | Understanding the Mean, Median & Mode. Scribbr. Retrieved 16 February 2026, from https://www.scribbr.co.uk/stats/measures-of-central-tendency/
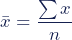
 : sum of all values in the sample dataset
: sum of all values in the sample dataset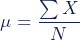
 : sum of all values in the population dataset
: sum of all values in the population dataset